Variants-trait association
The core objective of genetic studies is to identify which genetic variants contribute to disease risk. While establishing direct causation is challenging, we can detect statistical associations between genetic variants and traits by analyzing large-scale genomic data.
Large biobanks (such as the UK Biobank) have collected genomic data from hundreds of thousands of samples. To study variant-trait associations, one approach is to apply linear or logistic regression for each genetic variant, treating genotypes as independent variables and the trait as the dependent variable.
If we define G as our genotype matrix, y as our phenotype vector, and X as our covariate matrix (including age, sex, and principal components), we can perform a GWAS using the following R pseudo code (of course you should use PLINK for a realistic analysis):
# for continuous
for (SNP in 1:ncol(G)) {
model <- lm(y ~ G[, SNP] + X)
p_value[SNP] <- summary(model)$coefficients[2, 4] # Extract p-value for SNP
}
# for binary
for (SNP in 1:ncol(G)) {
model <- glm(y ~ G[, SNP] + X, family = "binomial")
p_value[SNP] <- summary(model)$coefficients[2, 4] # Extract p-value for SNP
}
GWAS with scaled data
Statistical geneticists often scale genotypes and phenotypes before GWAS analysis. This procedure can simplify the mathematics, and has a few important consequences. They also tend to parameterize the model with heritability. Let’s define some notations that we will use here, and in future blog posts.
$$
\begin{split} G: &\text{ standardized genotype matrix} \\ y: &\text{ standardized phenotype} \\ \lambda, \hat\lambda: &\text{ true and estimated causal effect sizes} \\ \beta, \hat\beta: &\text{ true and estimated marginal effect sizes} \\ R: &\text{ LD matrix/ correlation matrix} \\ h^2: &\text{ narrow sense heritability} \\ N: &\text{ sample size} \\ M: &\text{ number of variants } \\ \end{split}
$$
The model we are considering is
$$
\begin{split} y &= G \lambda + \varepsilon \\ \varepsilon &\sim N(0, (1 - h^2) I) \end{split}
$$
Assuming each variant only explains a tiny bit of phenotypical variation, I present a few important results:
-
GWAS effect size estimates is
\(\hat \beta = \frac{1}{N}G^Ty\). -
GWAS standard error is a constant
\(s.e. = 1/\sqrt{N}\). -
GWAS z score is
\(\hat\beta \sqrt{N}\). -
LD is
\(R = \frac{G^T G}{N}\). it is not always invertable, but we can add a small diagonal matrix as for regularization. -
multiple regression results is
\(\hat \lambda = R^{-1} \hat \beta\). -
The underlying genetic value is
\(G \lambda\), therefore the heritability is defined as\(h^2 = \frac{\lambda^T G^T G \lambda}{N} = \lambda^T R \lambda = \beta^T R^{-1} \beta\) -
\(\hat \lambda\)is an unbiased estimator of\(\lambda\). More specifically,\(\hat \lambda \sim MVN(\lambda, \frac{1 - h^2}{N} R^{-1} )\) -
\(\hat \beta\)is an unbiased estimator of\(\beta\), More specifically,\(\hat \beta = R \hat \lambda \sim MVN(R\lambda, \frac{1 - h^2}{N} R)\). The diagonal elements are squared standard error of individual marker, which is usually close enough to\(1/N\)when heritability is small
Additionally, due to the sample size is typically large in GWAS, any additional degree of freedom will be ignored. Therefore, it is uncommon to see d.o.f adjustment like \(n - k\) in GWAS. In other words, we are performing asymptotic inference in GWAS.
Surprisingly, covariates are often ignored in the formulation: \(y = G \lambda + \varepsilon\). To ignore covariates, we either need to regress out covariates, or assume \(\mathbb{C}ov[G, \varepsilon] \neq 0\).
Simulation
Here is a demonstration of scaled GWAS using simulated data:
- generated genotypes for 1000 individuals, each with 74 variants.
######### Step1: Simulate genotypes
path = "https://www.mv.helsinki.fi/home/mjxpirin/GWAS_course/material/APOE_1000G_FIN_74SNPS."
haps = read.table(paste0(path,"txt"))
info = read.table(paste0(path,"legend.txt"),header = T, as.is = T)
n = 1000 # number of samples
p = ncol(haps) # number of variants
G = as.matrix(haps[sample(1:nrow(haps), size = n, repl = T),] +
haps[sample(1:nrow(haps), size = n, repl = T),])
row.names(G) = NULL
colnames(G) = NULL
G_ = scale(G)
- pick 3 variants to be causal, and generate phenotypes
######### Step2: Simulate phenotypes
# pick 3 causal variants, and assign effect size
lambda = rep(0, ncol(G_))
causal_SNPs_idx = c(3, 18, 65)
causal_SNPs_eff = c(0.3, -0.1, 0.15)
lambda[causal_SNPs_idx] = causal_SNPs_eff
R = t(G_) %*% G_ /n # LD matrix
h2 = t(lambda) %*% R %*% lambda # heritability
err = rnorm(n, mean = 0, sd = sqrt(1 - h2))
y = G_ %*% lambda + err
y_ = scale(y)
- show key results
######### Step3: key results
beta_hat = 1/n * t(G_) %*% y_ # GWAS effect size estimates
z = sqrt(n) * beta_hat # z-score estimates
se = 1/sqrt(n) # standard error
pval = pchisq(z^2, df = 1, lower.tail = F) # p value
beta = R %*% lambda # marginal effect size
# visualize Manhattan plot
colors <- ifelse(lambda == 0, "black", "red")
plot(x = 1:p, y = -log10(pval), main = "Manhattan plot",
xlab = "Variant", ylab = "-log10(p)", col = colors, bg = colors, pch = 21)
legend("topright", legend = c("Causal variants", "Non-causal variants"),
pch = 21, pt.bg = c("red", "black"), col = c("red", "black"),
pt.cex = 1.5, cex = 0.8, bty = "n")
abline(h = -log10(5e-8), col = "grey", lty = 2)
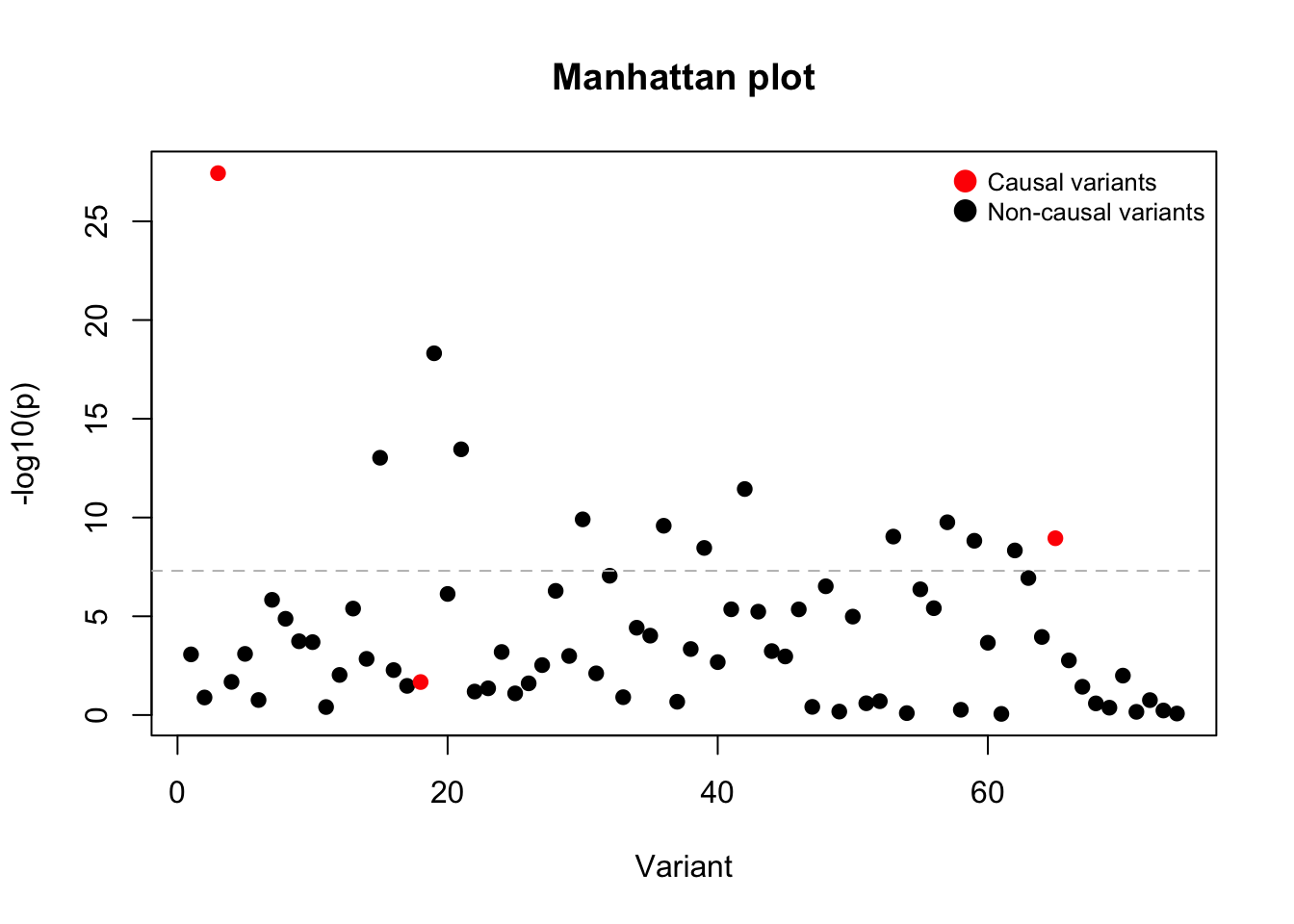
I want to highlight two important observations:
- Non-causal variants can be significantly associated with the traits (due to linkage with causal variants)
- Causal variants can be non-significant (due to insufficient power)
By regressing the phenotype with each variants, we can nominate trait-associated variants. Additionally, these summary statistics allows us to estimate the heritability of a trait. One way is to apply \(\hat h^2 = \hat \beta^T R^{-1} \hat \beta\), but this approach relies on inverting the LD matrix, which is practically impossible. Another practical approach is to use the variants with the most significant p value to estimate \(h^2\).
h2 # real h2
## [,1]
## [1,] 0.1355976
const = 1e-6
t(beta_hat) %*% solve(R + const* diag(p)) %*% beta_hat # estimated h2 using all variants
## [,1]
## [1,] 0.2054077
top_var = order(pval)[1]
var(G_[,top_var] * beta_hat[top_var]) # estimated h2 using the top variant
## [1] 0.1210901
Reference:
I learned these concepts largely through Matti Pirinen’s fantastic tutorials. I kept the notations to be consistent with his notations.