LDSC derivation
We discussed how to perform GWAS with scaled genotypes & phenotype. In this blog post, I present an important piece of result: Linkage Disequilibrium Score Regression (LDSC)
LDSC was proposed in this landmark paper, in which it described how LD affect the probability of a variant being significant. Under infinitesimal model, LDSC states \(\mathbb{E}[\chi_j^2] = \frac{Nh^2}{M} l_j + 1\), where \(l_j \equiv \sum_{k = 1}^M r_{jk}^2\) is the LD score. To carry out the derivation, one must treat the effect size as random: \(\lambda_j \sim N(0, \frac{h^2}{M})\).
In GWAS, the marginal effect size estimates (condition on true marginal effect size) is normally distributed: \(\hat \beta_j | \beta_j \sim N(\beta_j, \frac{1}{N})\). Equivalently, \(\hat \beta_j | \lambda \sim N(\sum_{k = 1}^{M} r_{jk} \lambda_k, \frac{1}{N})\).
I first state some quantities that will be useful for the derivations. Those quantities should be easy to varify:
$$
\begin{split} \mathbb{E}[\lambda_j] &= 0 \\ \mathbb{E}[\lambda_j^2] &= \frac{h^2}{M} \\ \mathbb{E}[\hat \beta_j | \lambda_j] &= \sum_{k = 1}^{M} r_{jk} \lambda_k \\ \mathbb{V}ar[\hat \beta_j | \lambda_j] &= \frac{1}{N} \\ \mathbb{E}[\hat \beta_j^2 | \lambda_j] &= \mathbb{V}ar[\hat \beta_j | \lambda_j] + \mathbb{E}^2[\hat \beta_j | \lambda_j] = \frac{1}{N} + (\sum_{k = 1}^{M} r_{jk} \lambda_k )^2 \end{split}
$$
Before we investigate \(\mathbb{E}[\chi_j^2]\), let’s express \(\mathbb{E}[\hat \beta_j^2]\):
$$
\begin{split} \mathbb{E}[\hat \beta_j^2] &= \mathbb{E}[ \mathbb{E}[\hat \beta_j^2 \mid \lambda]] \\ &= \mathbb{E}[\frac{1}{N} + (\sum_{k = 1}^{M} r_{jk} \lambda_k )^2] \\ &= \frac{1}{N} + \mathbb{E}[ (\sum_{k = 1}^M r_{jk} \lambda_k)^2 ] \\ &= \frac{1}{N} + \mathbb{E}[ (r_{j1} \lambda_1 + r_{j2} \lambda_2 + ...)^2 ] \\ &= \frac{1}{N} + \mathbb{E}[ \sum_{k = 1}^{M} (r_{jk} \lambda_k )^2 + 2 \cdot \sum_{p \neq q} r_{jp} r_{jq} \lambda_p \lambda_q ] \\ &= \frac{1}{N} + \sum_{k = 1}^M r_{jk}^2 \cdot \frac{h^2}{M} \\ &= \frac{h^2}{M} l_j + \frac{1}{N} \end{split}
$$
Further,
$$
\begin{split} \mathbb{E}[\chi_j^2] & = \mathbb{E}[(\frac{\hat \beta_j}{1/ \sqrt{N}})^2] \\ &= N \mathbb{E}[\hat \beta_j^2] \\ &= \frac{Nh^2}{M} l_j + 1 \end{split}
$$
The derivation took the insight that only marginal effect size are observed. Therefore, we investigate the statistical property of the marginal distribution of marginal effect sizes (a.k.a \(p(\hat \beta)\), but not the conditional distribution \(p(\hat \beta \mid \lambda)\)). Biologically, if one variant has more LD friends, then it is more likely to be significant. LDSC has been further extended to study binary traits, partition heritability, and genetic correlation between traits.
Simulation
Here is a simulation I have (with some code borrowed from Matti Pirinen’s incredible tutorial).
path = "https://www.mv.helsinki.fi/home/mjxpirin/GWAS_course/material/APOE_1000G_FIN_74SNPS."
haps = read.table(paste0(path,"txt"))
info = read.table(paste0(path,"legend.txt"),header = T, as.is = T)
n = 1000
G = as.matrix(haps[sample(1:nrow(haps), size = n, repl = T),] + haps[sample(1:nrow(haps), size = n, repl = T),])
row.names(G) = NULL
colnames(G) = NULL
G_ = scale(G)
h2 = 0.05
R = t(G_) %*% G_ /n # LD matrix
get_chi2<- function(G_, h2, R){
lambda = rnorm(ncol(G_), mean = 0, sd = sqrt(h2/ncol(G_)))
err = rnorm(n, mean = 0, sd = sqrt(1 - h2))
y = G_ %*% lambda + err
y_ = scale(y)
##
beta_hat = t(G_) %*% y / n
chi2 = n * beta_hat^2
return(as.vector(chi2))
}
# do this 300 times, and average them to get the expectation
chi2_simulations = replicate(n = 300, get_chi2(G_, h2, R))
exp_chi2 = rowMeans(chi2_simulations)
ldsc = rowSums(R^2)
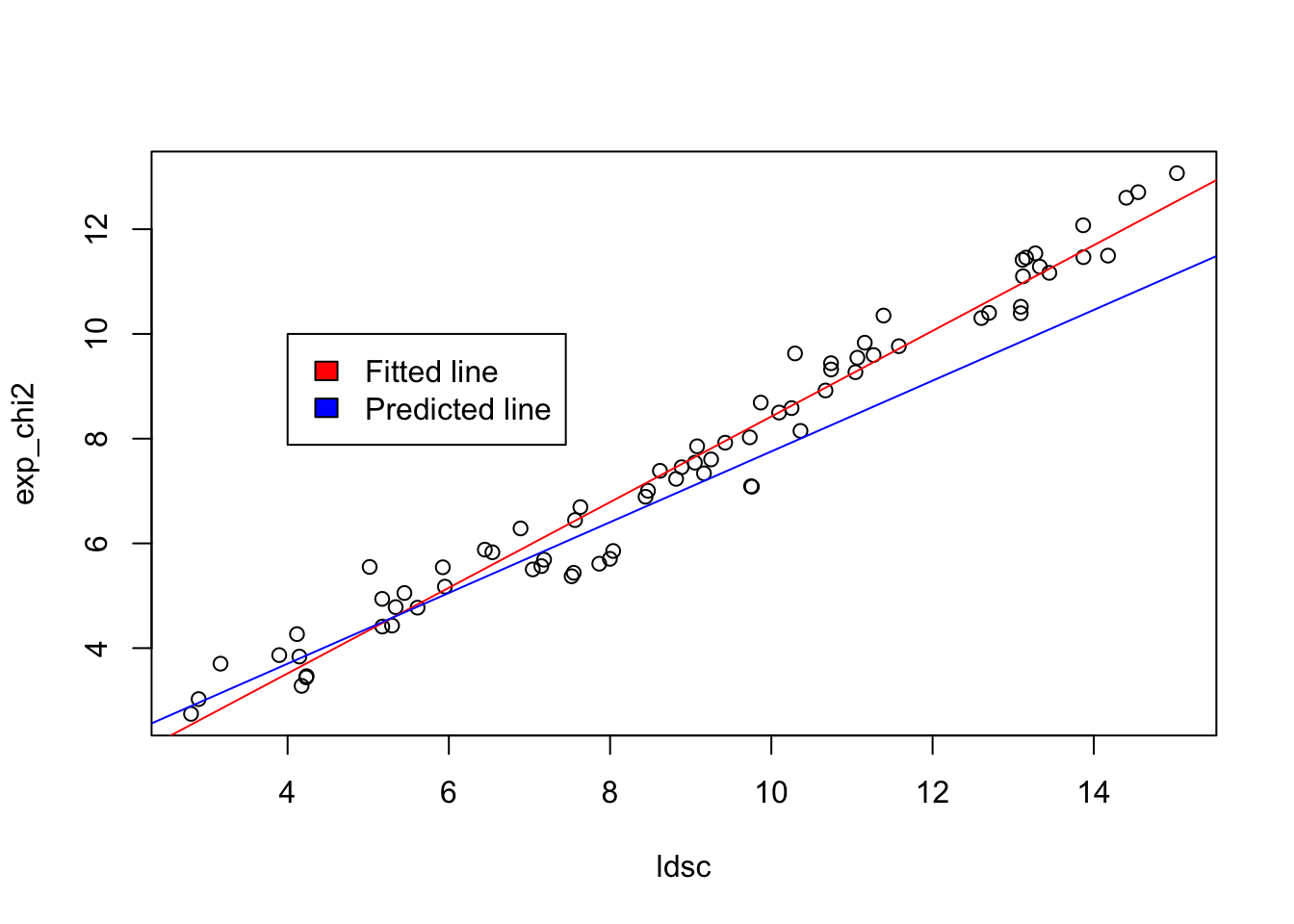
plot(ldsc, exp_chi2)
abline(lm(exp_chi2 ~ ldsc), col = "red")
abline(a = 1, b = (n * h2 / ncol(G)), col = "blue")
legend(4, 10, legend=c("Fitted line", "Predicted line"),
fill = c("red","blue"))
Reference:
I also thank Arslan Zaidi’s comment to correct my simulations