An Intuitive Explanation of Bayesian Network
Introduction
Bayesian network, a probabilistic model that represents the causal relationship between variables, has gain its popularity in various fields. In biology, for example, people start to use this model to infer genetic regulatory network (GRN) due to its nice property of being directional. The aim of this blog post is to provide a gentle and less-mathematical introduction to Bayesian network.
An example
Suppose we are going to take a math exam next week. The outcome of the exam heavily depends on two factors: sleep and study. If we study and sleep well, chances are high that we will do a good job in the exam. Also, sleep can affect our attention and therefore influence our study quality. Since the world is probabilistic, we need to define the probability of each action (sleep, study and exam):
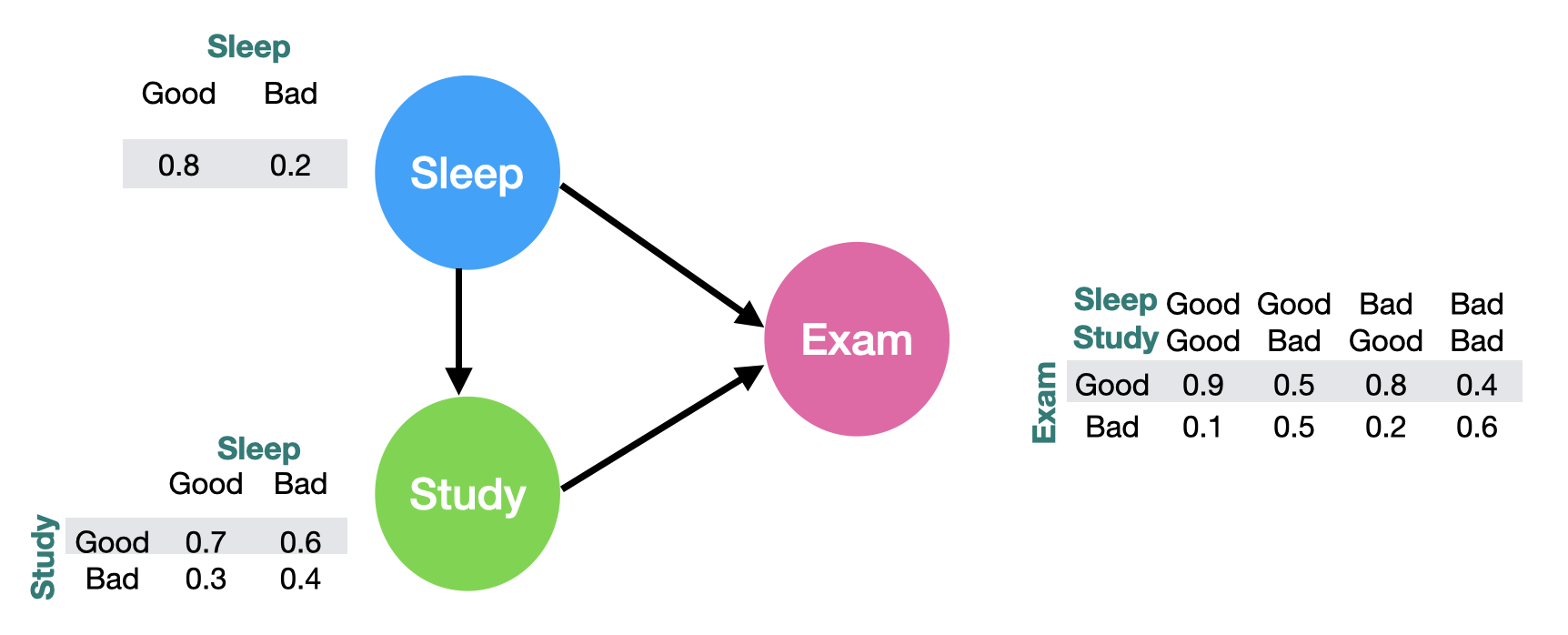
The graph is easy to interpret: for example, the probability that we have a good sleep is 80%; the probability of we study well given that we slept well is 70%; the probability of we perform well in the exam, given we slept well and studied well is 90%, etc… Notice that each column should sum up to 1 to make sure the probability is valid.
Inference
Suppose we have finished the exam and we Aced it! Your teacher looked at your grade, and asked a question: did you sleep well recently? Equivalently, our teacher asked what is $$P (\text{Sleep = good}|\text{Exam = good})$$
In this section, we will try to answer this question by carefully examine each term, and calculate the probability based on the graph above.
To answer this question, we can list all possible combinations of $(\text{Sleep, Study})$ when we did well in our exam. Here is the calculation:
For example, to calculate the probability of Sleep well, Study well, and Exam well, we have $$ \begin{aligned} & P(\text{Sleep = G, Study = G, Exam = G}) \\ &= P(\text{Sleep = G}) \times P(\text{Study = G | Sleep = G}) \times P(\text{Exam = G | Sleep = G, Study = G}) \\ &=0.8 \times 0.7 \times 0.9 \\ &= 0.504 \end{aligned} $$
Similarly, we can calculate the probability of other combination of Sleep and Exam, when we did well in our exam
$P(\text{Sleep = G, Study = B, Exam = G}) = 0.8 \times 0.3 \times 0.5 = 0.12$ $P(\text{Sleep = B, Study = G, Exam = G}) = 0.2 \times 0.6 \times 0.8 = 0.096$ $P(\text{Sleep = B, Study = B, Exam = G}) = 0.2 \times 0.4 \times 0.4 = 0.032$
According to conditional probability formula, we have:
$$P (\text{Sleep = G}|\text{Exam = G}) = \frac{P (\text{Sleep = G} \cap \text{Exam = G})}{P (\text{Exam = G})} $$
We have already listed all possible combinations of $P (\text{Exam = G})$ above, so the denominator is: $$P (\text{Exam = G}) = 0.504 + 0.12 + 0.096 + 0.032 = 0.752$$
To calculate $P (\text{Sleep = G} \cap \text{Exam = G})$, we have two different scenarios:$$P(\text{Sleep = G, Study = G, Exam = G}) + P(\text{Sleep = G, Study = B, Exam = G}) \\ = 0.504 + 0.12 = 0.624$$
The final answer is $P (\text{Sleep = good}|\text{Exam = good}) = \frac{0.624}{0.752} = 0.83$
Inference by sampling
So far the calculation isn’t crazy, but many times the Bayesian network can have hundreds of nodes and edges. Calculating the exact conditional probability for a large network is often unmanageable. In fact, it has been proven that Bayesian network inference is a NP problem, meaning the complexity grows exponentially.
A more feasible way of inferring bayesian network is to draw samples from the network, and we estimate the conditional probability based on our samples.
Here I provide some R code that can simulate this network, and the answer should be very close to the above result:
# define a function that simulate the Bayesian network
Simulate = function(){
# define probability of sleep
SLEEP = rbinom(1, size = 1, prob = 0.8)
# define conditional probability of study
if (SLEEP == 1){
STUDY = rbinom(1, size = 1, prob = 0.7)
}else{
STUDY = rbinom(1, size = 1, prob = 0.6)
}
# define conditional probability of exam
if (SLEEP == 1 & STUDY == 1){
EXAM = rbinom(1, size = 1, prob = 0.9)
} else if (SLEEP == 1 & STUDY == 0){
EXAM = rbinom(1, size = 1, prob = 0.5)
} else if (SLEEP == 0 & STUDY == 1){
EXAM = rbinom(1, size = 1, prob = 0.8)
} else if (SLEEP == 0 & STUDY == 0){
EXAM = rbinom(1, size = 1, prob = 0.4)
}
return(c(SLEEP, STUDY, EXAM))
}
# create an empty table to store results
Simulate_res = matrix(nrow = 0, ncol = 3)
# simulate 100000 times; this process takes about 1 minute.
for (i in 1:100000){
Simulate_res = rbind(Simulate_res, Simulate())
}
# calculate the conditional probability
sum((Simulate_res[,3] == 1) & (Simulate_res[,1] == 1))/ sum(Simulate_res[,3] == 1)
An R package for Bayesian network
Here I also provide some code that I adapted from the tutorial of $bnlearn$ package. I constructed the Bayesian network and defined the probability distribution for each node. $bnlearn$ can make the inference process much easier. It also provide functionalities that enables us to learn from data (hopefully I can cover this topic in the future).
library(bnlearn)
# define the structure of the network
dag <- empty.graph(nodes = c("Sleep","Study", "Exam"))
arc.set <- matrix(c("Sleep", "Study",
"Sleep", "Exam",
"Study", "Exam"),
byrow = TRUE, ncol = 2,
dimnames = list(NULL, c("from", "to")))
arcs(dag) <- arc.set
# plot the network
graphviz.plot(dag, layout = "dot")
# define the probability for each node
Sleep.lv <- c("good", "bad")
Study.lv <- c("good", "bad")
Exam.lv <- c("good", "bad")
Sleep.prob = array(c(0.8,0.2), dim = 2, dimnames = list(Sleep = Sleep.lv))
Study.prob = array(c(0.7,0.3,0.6,0.4), dim = c(2,2), dimnames = list(Study = Study.lv, Sleep = Sleep.lv))
Exam.prob = array(c(0.9,0.1,0.5,0.5, 0.8, 0.2, 0.4, 0.6), dim = c(2,2,2), dimnames = list(Exam = Exam.lv, Study = Study.lv, Sleep= Sleep.lv))
cpt <- list(Sleep = Sleep.prob, Study = Study.prob, Exam = Exam.prob)
# build the network
bn <- custom.fit(dag, cpt)
# inference
cpquery(bn, event = (Sleep == "good"), evidence = (Exam == "good"))