Dive into Bayesian statistics (5): Intro to PyMC3

2021-11-22 487 words 3 minutes

Contents

In our previous post, we have manually implemented the Markov Chain Monte Carlo algorithm (specially, Metropolis Hastings), and drew samples from the posterior distribution. The code isn’t particularly difficult to understand, but it’s not intuitive to read/write neither. Besides the difficulty of implementation, algorithm performance (a.k.a speed) is also a major consideration in a more realistic application. Luckily, well-written tools are available to resolve these obstacles, namely, Stan and PyMC3.

Subjectively speaking, Stan is not my cup of tea. I remembere I spent the entire afternoon trying to install R Stan while still failed. What makes it worse is that Stan defined its own language, which adds another layer of complexity. In contrast, PyMC3 is much easier to install. The documentations and tutorials are well-written, and people with some understanding of Bayesian stas should be able to follow them without much trouble. In this post, and posts of the future, I will stick with PyMC3.

(p.s. I am by no means an expert of Bayesian stats and PyMC3, so if you find any pieces of code that looks strange, don’t hesitate to comment below.)

Import modules

# if you haven't installed PyMC3 yet, simply do
# pip install pymc3
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
from pymc3 import *
import seaborn as sns

Data

This is the data we have been using so far.

x = np.array([5,3,4,6])

Build the model, Sampling from the posterior distribution

with Model() as model:  
    # Define priors
    Poiss_lambda = Gamma("Poiss_lambda", alpha=2, beta=2)

    # Define likelihood
    likelihood = Poisson("x", mu =  Poiss_lambda, observed=x)

    # Inference
    trace = sample(3000, cores=2)  # draw 3000 posterior samples

Plot

plt.figure(figsize=(7, 7))
plot_trace(trace)
plt.tight_layout();

Notice that the picture is almost identical as what I drew before. On the left side, you see the density plot (which could be interpreted as a smooth histogram), where we can find the peak when $\lambda \approx 3.2$. The right-hand side picture is simply a random walk of $\lambda$, which can be used to determine if the sampling is stable.

Maximum A Posteriori

Of course we can use PyMC3 to find the parameters that give the maximum posteriori. The code is simple:

pm.find_MAP(model=model)

Unsurprisingly, we get:

{'Poiss_lambda_log__': array(1.15267951), 'Poiss_lambda': array(3.16666667)}

,which is the same as what we have calculated here

Posterior Predictive Distribution

To sample the posterior predictive distribution, type

# sampling 
with model:
    ppc = pm.fast_sample_posterior_predictive(trace,var_names =["x"])
    
# draw histogram
sns.histplot(x=ppc["x"].flatten(), binwidth = 1)

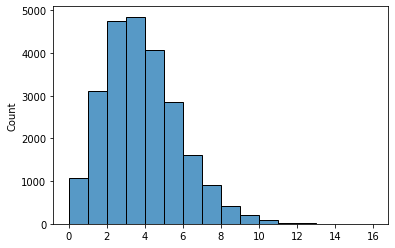
Again, the shape of the histogram is what we have seen before, which further validated our results.

Summary

So far we have covered the fundamentals of Bayesian inference, which includes topics like:

In the next few posts, I will switch gears and cover some other interesting topics like Hidden Markov Chain, Singular Value Decomposition, etc.

It will be fun, and stay tuned.